A review on mathematical models for estimating indoor radon concentrations

Ji Hyun Park; Dae Ryong Kang; Jinheum Kim

doi:10.1186/s40557-016-0091-6

Articles

Page Path: HOME > Ann Occup Environ Med > Volume 28; 2016 > Article

Review A review on mathematical models for estimating indoor radon concentrations: Ji Hyun Park, Dae Ryong Kang, Jinheum Kim; Annals of Occupational and Environmental Medicine 2016;28:7.
DOI: https://doi.org/10.1186/s40557-016-0091-6
Published online: February 25, 2016

Department of Mathematics, Ajou University, Suwon, 16499 South Korea

Department of Humanities and Social Medicine, Ajou University School of Medicine, Suwon, 16499 South Korea

Department of Applied Statistics, University of Suwon, Hwaseong, 18323 South Korea

• Received: January 18, 2016 • Accepted: February 18, 2016

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated.

52 Views
1 Download
8 Web of Science
8 Crossref
11 Scopus

prev next

Full Article

Download PDF

Abstract
Background
Review
Conclusions
Acknowledgements
NOTES
References

Abstract

Radiation from natural sources is one of causes of the environmental diseases. Radon is the leading environmental cause of lung cancer next to smoking. To investigate the relationship between indoor radon concentrations and lung cancer, researchers must be able to estimate an individual’s cumulative level of indoor radon exposure and to do so, one must first be able to assess indoor radon concentrations. In this article, we outline factors affecting indoor radon concentrations and review related mathematical models based on the mass balance equation and the differential equations. Furthermore, we suggest the necessities of applying time-dependent functions for indoor radon concentrations and developing stochastic models.
Keywords:
Keywords
Mathematical model; Indoor concentration; Radon entry; Exposure

Background

Exposure to radiation from natural sources leads to various environmental diseases. Radon, which is the primary constituent of natural radiation [1], is the leading environmental cause of lung cancer next to smoking [2]. Studies in Europe, the United States, Canada, and China have effectively shown a relationship between indoor radon concentrations and lung cancer [3].

To establish a relationship between indoor radon concentrations and lung cancer, estimating an individual’s cumulative indoor level of radon exposure is necessary. For a period of time, t₁ to t₂, an individual’s cumulative level of indoor radon exposure can be defined as

where C_i(t) is the indoor radon concentration (Bq/m³) at time t and V is the volume of the building of interest (m³). 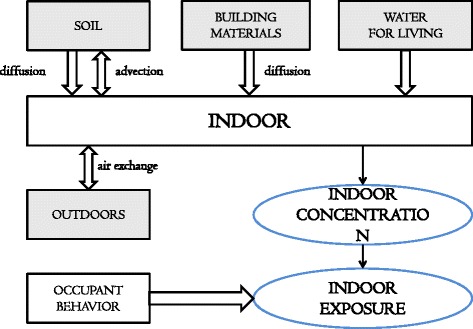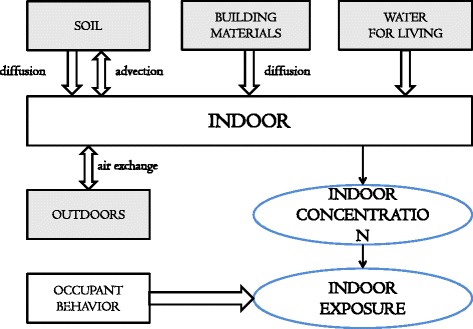C_i(t) can be affected by several factors: The United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) reported that the 56 % of the radon that enters into a building comes from the soil, 21 % from building material (BM), 20 % from outdoor air, 2 % from a building’s water supply, and 1 % from natural gas [4]. As shown in Fig. 1 (see [5, 6] for more details), radon in the soil permeates a building: diffusive and advective flow; radon from BM diffuses into buildings. A building’s water supply and natural gas are also sources that introduce radon into a building, although that from natural gas is not generally considered because it is difficult to measure and contributes to only very small concentrations. Additionally, indoor radon concentrations can also vary as a result of air exchange between indoor and outdoor air.

Fig. 1

Diagram of factors governing indoor radon concentrations and exposure^a. ^aThis diagram was modified from Font [5] and Font and Baixeras [6]. Radon in the soil permeates a building: diffusive and advective flow; radon from BM diffuses into buildings. A building’s water supply and natural gas are also sources that introduce radon into a building, although that from natural gas is not generally considered because it is difficult to measure and contributes to only very small concentrations. Additionally, indoor radon concentrations can also vary as a result of air exchange between indoor and outdoor air. Therefore, a subject’s indoor radon exposure in a building can be mainly determined by his or her behaviour and indoor radon concentration of the building that he or she resides

There had been several studies to estimate the indoor radon concentrations with mathematical models. Ramola et al. [7] estimated the indoor radon concentration using a mathematical model based on the radon flux in soil and groundwater. Arvela et al. [8] calculated the indoor radon concentrations with a mathematical model which considers diffusion from soil and BM sources and air exchange simultaneously. These calculations have been compared with the measured variations of Finnish dwellings. Font [5] and Font and Baixeras [6] developed a generic and dynamic model of Radon Generation, Entry, and Accumulation indoors (RAGENA) which describes all the known sources including soil, BM, and water, and this model has been adapted to a Mediterranean climate house and Swedish house [9, 10]. Mathematical models for estimating indoor radon concentrations in high-rise buildings have been conducted by Man and Yeung [11] and Shaikh et al. [12]. These models included the contributions from BM and outdoor air. Moreover, model of indoor radon concentration in thermal spas was developed by Vogiannis and Nikolopoulos [13].

Most of the mathematical models reviewed in this article are based on the mass balance equation and differential equations. They can all be solved by numerical methods. The notation included in the mathematical equations reviewed in this article is listed in Table 1.

Table 1

Notation

Symbol	Unit	Description
C _bm	Bq/m³	Radon concentration in building material (BM)
C _i	Bq/m³	Indoor radon concentration
C _o	Bq/m³	Radon concentration of outdoor air
C _s	Bq/m³	Radon concentration in soil
C _w	Bq/m³	Radon concentration in water supply
F _s	Bq/(m² · s)	Total radon flux from soil into building
k _a	m/(s · Pa)	Advection transfer coefficient of soil
k _d,bm	m/s	Diffusion transfer coefficient of BM
k _d,s	m/s	Diffusion transfer coefficient of soil
q _ij	m³/s	Air current from compartment i to compartment j
S _bm	m²	Indoor surface area of radon containing BM
S _g	m²	Building area towards ground
t _w	dimensionless	Radon transfer efficiency of water supply
U _w	m³/s	Use rate of water
V	m³	Volume of the indoor
ΔP _s − i	Pa	Soil-indoor pressure difference
λ	1/s	Radon decay constant
λ _v	1/s	Ventilation rate

Review

Most of the references reviewed in this article developed models for evaluating indoor radon concentrations based on the following mass balance equation:

According to the above, changes in indoor radon concentrations are affected by the sources of radon entry, building ventilation (radon exchange), and decay reaction. First, we introduce a model for assessing indoor radon concentrations attributed to the three main sources of radon entry (soil, BM, and water) and decay reaction.

Radon entry and decay reaction

Soil

First, we will consider a single-room building. As mentioned above, indoor radon concentrations are mainly affected by radon in the soil [4]. Accordingly, the change in indoor radon concentration for an infinitesimal time can be described as

1

where the first and the second terms describe changes caused by radon in the soil and radioactive decay, respectively (see [5, 6, 9, 10, 14, 15] for more details). The total radon flux from the soil into the building F_s in Equation (abbre. Eq.) (1) can be calculated as

2

where the first and the second terms in the right-hand side of Eq. (2) describe diffusive and advective flow, respectively. Substituting Eq. (2) into Eq. (1), we obtain the following equation:

3

Although radon from groundwater contributes very little to indoor radon, it can constitute an important source in specific instances; the total radon flux from the ground, considering both radon in soil and groundwater, can be found in Ramola et al. [9]. In the meantime, Font [5] and Font and Baixeras [6] suggested evaluating total radon flux from the soil into the building F_s differently: the soil can be divided into two compartments, disturbed soil (DS, the volume of soil underneath a building from which radon can reach the basement of the building by diffusion and pressure driven flow) and undisturbed soil (US, the soil attached to the DS that is not influenced by the presence of the building). The radon concentrations in the US and in the DS are described in [5, 6]. However, for simplicity, throughout this article we develop a model using a total radon flux into the building that consider only DS, namely F_s in Eq. (2).

Building material

Next, we consider BM which is second leading source of radon into a building after soil. In some instances, BM can be the greater source of radon entry than the soil, such as in high-rise buildings [11, 12]. As illustrated in Fig. 1, radon entry from BM occurs through diffusion, as the difference in indoor and BM radon concentrations. Thus, the change in indoor radon concentration stemming from BM for an infinitesimal time can be described as

4

(see [5, 6, 8, 10–12] for more details).

Water for living

Indoor radon concentrations can also depend on the amount of radon in a building’s water supply. In general, the influence of radon from a water supply on indoor radon concentrations is low; however, extremely high concentrations of radon in a water supply, when present, must be taken into consideration. To do so, changes in indoor radon concentrations caused by radon in a building’s water supply for an infinitesimal time can be taken as

5

(see [5, 6, 13] for more details).

Then, from Eqs. (3), (4) and (5), the rate of change in indoor radon concentrations attributed to all sources of radon entry and decay can be represented by

6

where dC_i = C_i(t + dt) − C_i(t) and dt denotes an infinitesimal time.

Radon exchange

Ventilation between indoor and outdoor air

As stipulated in the mass balance equation, radon exchange caused by ventilation and differences in indoor and outdoor radon concentrations must be considered. In general, indoor radon concentrations are higher in the winter season, compared to those in other seasons. This phenomenon is likely to be primarily related with ventilation. In considering radon exchange between indoor and outdoor air, we expand the model for assessing indoor radon concentration in Eq. (6) as

7

[TeX:] \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{d{C}_i}{dt}=\left\{{k}_{d,s}\left({C}_s-{C}_i\right)+{k}_a\varDelta {P}_{s-i}{C}_s\right\}\frac{S_g}{V}+{k}_{d,bm}\left({C}_{bm}-{C}_i\right)\frac{S_{bm}}{V}+\frac{C_w{U}_w{t}_w}{V}-{\lambda}_v\left({C}_i-{C}_o\right)-\lambda {C}_i, $$\end{document}dCidt={kd,s(Cs−Ci)+kaΔPs−iCs}SgV+kd,bm(Cbm−Ci)SbmV+CwUwtwV−λv(Ci−Co)−λCi,

where λ_v(C_i − C_o) describes the radon exchange between indoor and outdoor air [5, 6, 9–16]. In Eq. (7), one may assume that λ = 0 because λ is relatively smaller than λ_v.

Ventilation among the compartments

Additionally, we must treat a building as a collection of different N compartments for more realistic models. In this case, from Eq. (7) the model for indoor radon concentration of i th compartment is derived as

8

[TeX:] \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \frac{d{C}_i}{dt}=\left\{{k}_{d,s}\left({C}_s-{C}_i\right)+{k}_a\varDelta {P}_{s-i}{C}_s\right\}\frac{S_g}{V}+{k}_{d,bm}\left({C}_{bm}-{C}_i\right)\frac{S_{bm}}{V}+\frac{C_w{U}_w{t}_w}{V}-{\lambda}_v\left({C}_i-{C}_o\right)-\lambda {C}_i-{\displaystyle \sum_{\begin{array}{c}\kern1em j=1\kern1em \\ {}\kern1em j\ne i\kern1em \end{array}}^N}\left({q}_{ij}{C}_i-{q}_{ji}{C}_j\right)\frac{1}{V}, $$\end{document}dCidt={kd,s(Cs−Ci)+kaΔPs−iCs}SgV+kd,bm(Cbm−Ci)SbmV+CwUwtwV−λv(Ci−Co)−λCi−∑j=1j≠iN(qijCi−qjiCj)1V,

where the last term describes the radon exchange between compartments i and j [5, 6].

When developing a model for assessing indoor radon concentrations of an actual building, some sources of radon entry and radon exchange may be removed from or added to Eq. (8) in accordance with the surroundings and the characteristics of the building. When adapting the model to an actual building, parameters other than the indoor radon concentration can either be measured or obtained from published data or certain time variation functions. To estimate indoor radon concentrations, one may seek to apply the following methods: obtaining the explicit solution of the differential equation at a steady state and using a proper numerical method that is usually based on a finite difference or finite element solutions to the equations. The models referenced in this review are summarized in Table 2.

Table 2

Summary of references reviewed in this article

Author(s)	Year	Factor				Application	Method^a
Author(s)	Year	Soil	BM	Water	Vent.	Application	Method^a
Kusuda et al. [16]	1980	-	-	-	○	Sample calculations	N.S.
Capra et al. [14]	1994	-	-	-	○	An environmental chamber	N.S.
Ramola et al. [9]	2011	○	-	-	○	Budhakedar area of Garhwal Himalaya in summer and winter	N.S.S.
Man and Yeung [11]	1999	-	○	-	○	Newly constructed, uninhabited high-rise buildings in Hong Kong	N.S.S.
Shaikh et al. [12]	2003	-	○	-	○	A multi-storey building in Mumbai, India over four seasons	N.S.S.
Vogiannis and Nikolopoulos [13]	2008	-	-	○	○	Thermal spas in Greece	N.M.
Jelle [15]	2012	○	○	-	○	Sample calculations	N.S.S.
Arvela et al. [10]	1988	○	○	-	○	Finnish dwellings in summer and winter	N.S.S.
Font [5]	1997	○	○	○	○	Mediterranean climate house and Swedish house^b	N.M.
Font and Baixeras [6]	2003	○	○	○	○	Mediterranean climate house and Swedish house^b	N.M.

^aN.M., N.S., and N.S.S. mean the numerical method using specially developed computer codes, the numerical solution of the differential equation, and the numerical solution of the differential equation at a steady state, respectively

^bThese applications were discussed in [7, 8]

Conclusions

Mathematical models for estimating indoor radon concentrations provide not only a method of assessment but also an understanding between parameters that govern indoor radon levels. In order to estimate an individual’s cumulative indoor radon exposure, assessing indoor radon concentrations is necessary. To do so, one should seek to understand the mechanisms of radon entry and exchange in relation to side-specific surroundings and characteristics of a building. Accordingly, resultant models in consideration of said characteristics may be simpler than Eq. (8) or may necessitate additional research on factors of indoor radon concentrations (e.g., age of the BM and relative humidity).

Most of the models reviewed in this article utilized solutions at a steady state and considered parameters to be constant in order to estimate indoor radon concentrations. Such approaches are often adequate, as a steady state is rarely attained in actual buildings because of time-dependent factors (e.g., air exchange rates, which change with atmospheric conditions). For this reason, time-dependent solutions may be more accurate than steady state solutions in assessment of actual building conditions. Additionally, all of the models included in this review considered only deterministic models. However, a stochastic model designed to account for unrecognized factors and noise-corrupted measurements may offer better approximation of indoor radon levels.

Acknowledgements

This subject is supported by Korea Ministry of Environment (MOE) as “the Environmental Health Action Program” (Grant Number 2015001350002).

NOTES

Competing interests

The authors declare that they have no competing interests.

Authors’ contributions

JHP, the first author, searched the related references, drafted the initial manuscript, and corrected this manuscript. DRK supported and advised the epidemiological view. JK is a corresponding author and corrected this manuscript. All authors read and approved the final manuscript.

References

1. World Health Organization. Ionizing radiation in our environment. 2011, Geneva: World health.
2. http://yosemite.epa.gov/opa/admpress.nsf/6424ac1caa800aab85257359003f5337/8575b629701ce77b85257638005ef218!OpenDocument.
3. World Health Organization. WHO handbook on indoor radon: a public health perspective. 2009, Geneva: World Health Organization.
4. United Nations Scientific Committee on the Effects of Atomic Radiation. UNSCEAR Report 1993: Sources and effects of ionizing radiation. 1993, New York: United Nations.
5.
6. Ll F, Baixeras C. The RAGENA dynamic model of radon generation, entry and accumulation indoors. Sci Total Environ 2003;307(1):55–69. 12711425.Article PubMed
7. Font LI, Baixeras C, Domingo C, Fernández F. Experimental and theoretical study of radon levels and entry mechanisms in a Mediterranean climate house. Radiat Meas 1999;31(1):277–82. 10.1016/S1350-4487(99)00110-9.Article
8. Ll F, Baixeras C, Jönsson G, Enge W, Ghose R. Application of a radon model to explain indoor radon levels in a Swedish house. Radiat Meas 1999;31(1):359–62.Article
9. Ramola RC, Prasad G, Gusain GS. Estimation of indoor radon concentration based on radon flux from soil and groundwater. Appl Radiat Isot 2011;69(9):1318–21. 10.1016/j.apradiso.2011.04.025. 21596574.Article PubMed
10. Arvela H, Voutilainen A, Mäkeläinen I, Castrén O, Winqvist K. Comparison of predicted and measured variations of indoor radon concentration. Radiat Prot Dosimetry 1988;24(1–4):231–5.Article PDF
11. Man CK, Yeung HS. Modelling and measuring the indoor radon concentrations in high-rise buildings in Hong Kong. Appl Radiat Isot 1999;50(6):1131–5. 10.1016/S0969-8043(98)00128-6. 10355110.PubMed
12. Shaikh AN, Ramachandran TV, Vinod KA. Monitoring and modelling of indoor radon concentrations in a multi-storey building at Mumbai, India. J Environ Radioact 2003;67(1):15–26. 10.1016/S0265-931X(02)00144-3. 12633998.Article PubMed
13. Vogiannis E, Nikolopoulos D. Modelling of radon concentration peaks in thermal spas. application to Polichnitos and Eftalou spas (Lesvos Island—Greece). Sci Total Environ 2008;405(1):36–44. 10.1016/j.scitotenv.2008.06.029. 18715628.Article PubMed
14. Capra D, Silibello C, Queirazza G. Influence of ventilation rate on indoor radon concentration in a test chamber. J Environ Radioact 1994;24(3):205–15. 10.1016/0265-931X(94)90040-X.Article
15. Jelle BP. Development of a model for radon concentration in indoor air. Sci Total Environ 2012;416:343–50. 10.1016/j.scitotenv.2011.11.052. 22178027.Article PubMed
16. Kusuda T, Silberstein S, Mcnall PE. Modeling of radon and its daughter concentrations in ventilated spaces. J Air Pollut Control Assoc 1980;30(11):1201–7. 10.1080/00022470.1980.10465168.Article

Figure & Data

REFERENCES

Citations

Citations to this article as recorded by

Machine learning in environmental radon science
Javier Elío, Eric Petermann, Peter Bossew, Miroslaw Janik
Applied Radiation and Isotopes.2023; 194: 110684. CrossRef
Experimental Studies to Test a Predictive Indoor Radon Model
Simona Mancini, Martins Vilnitis, Nataša Todorović, Jovana Nikolov, Michele Guida
International Journal of Environmental Research and Public Health.2022; 19(10): 6056. CrossRef
General model for estimation of indoor radon concentration dynamics
Alla Dvorzhak, Juan Carlos Mora, Almudena Real, Carlos Sainz, Ismael Fuente
Environmental Science and Pollution Research.2021; 28(38): 54085. CrossRef
The 222Rn and 220Rn concentrations in some dwellings of Mandya city and its surroundings, Karnataka, India
Kesthur Naraseyappa Narasimhamurthy, Godekere Visweswaraiah Ashok, Thuruganur Siddaiah Shashi Kumar, Ningaiah Nagaiah
Indoor and Built Environment.2021; 30(8): 1295. CrossRef
A STUDY ON THE RADIATION DOSE DUE TO DISSOLVED 222RN IN WATER SAMPLES OF MANDYA CITY, KARNATAKA, INDIA
K N Narasimhamurthy, G V Ashok, T S Shashi Kumar, N Nagaiah, M B Karthik Kumar
Radiation Protection Dosimetry.2021; 194(2-3): 113. CrossRef
A Deterministic Model for Estimating Indoor Radon Concentrations in South Korea
Ji Hyun Park, Cheol Min Lee, Dae Ryong Kang
International Journal of Environmental Research and Public Health.2019; 16(18): 3424. CrossRef
Numerical modeling of the sources and behaviors of 222Rn, 220Rn and their progenies in the indoor environment—A review
Jun Hu, Guosheng Yang, Miklós Hegedűs, Kazuki Iwaoka, Masahiro Hosoda, Shinji Tokonami
Journal of Environmental Radioactivity.2018; 189: 40. CrossRef
Measurement and modeling of indoor radon concentrations in residential buildings
Ji Hyun Park, Sungim Whang, Hyun Young Lee, Cheol-Min Lee, Dae Ryong Kang
Environmental Health and Toxicology.2018; 33(1): e2018003. CrossRef

PubReader
ePub Link

Cite

CITE: export Copy Download Format; Close

Download Citation

Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.

Format:

RIS — For EndNote, ProCite, RefWorks, and most other reference management software
BibTeX — For JabRef, BibDesk, and other BibTeX-specific software

Include:

Citation for the content below
Citation and abstract for the content below

A review on mathematical models for estimating indoor radon concentrations

Ann Occup Environ Med. 2016;28:7 Published online February 25, 2016

DOI: https://doi.org/10.1186/s40557-016-0091-6

XML Download

Figure

A review on mathematical models for estimating indoor radon concentrations

Fig. 1 Diagram of factors governing indoor radon concentrations and exposurea. aThis diagram was modified from Font [5] and Font and Baixeras [6]. Radon in the soil permeates a building: diffusive and advective flow; radon from BM diffuses into buildings. A building’s water supply and natural gas are also sources that introduce radon into a building, although that from natural gas is not generally considered because it is difficult to measure and contributes to only very small concentrations. Additionally, indoor radon concentrations can also vary as a result of air exchange between indoor and outdoor air. Therefore, a subject’s indoor radon exposure in a building can be mainly determined by his or her behaviour and indoor radon concentration of the building that he or she resides

Fig. 1

A review on mathematical models for estimating indoor radon concentrations

Symbol	Unit	Description
C _bm	Bq/m³	Radon concentration in building material (BM)
C _i	Bq/m³	Indoor radon concentration
C _o	Bq/m³	Radon concentration of outdoor air
C _s	Bq/m³	Radon concentration in soil
C _w	Bq/m³	Radon concentration in water supply
F _s	Bq/(m² · s)	Total radon flux from soil into building
k _a	m/(s · Pa)	Advection transfer coefficient of soil
k _d,bm	m/s	Diffusion transfer coefficient of BM
k _d,s	m/s	Diffusion transfer coefficient of soil
q _ij	m³/s	Air current from compartment i to compartment j
S _bm	m²	Indoor surface area of radon containing BM
S _g	m²	Building area towards ground
t _w	dimensionless	Radon transfer efficiency of water supply
U _w	m³/s	Use rate of water
V	m³	Volume of the indoor
ΔP _s − i	Pa	Soil-indoor pressure difference
λ	1/s	Radon decay constant
λ _v	1/s	Ventilation rate

Author(s)	Year	Factor				Application	Method^a
Author(s)	Year	Soil	BM	Water	Vent.	Application	Method^a
Kusuda et al. [16]	1980	-	-	-	○	Sample calculations	N.S.
Capra et al. [14]	1994	-	-	-	○	An environmental chamber	N.S.
Ramola et al. [9]	2011	○	-	-	○	Budhakedar area of Garhwal Himalaya in summer and winter	N.S.S.
Man and Yeung [11]	1999	-	○	-	○	Newly constructed, uninhabited high-rise buildings in Hong Kong	N.S.S.
Shaikh et al. [12]	2003	-	○	-	○	A multi-storey building in Mumbai, India over four seasons	N.S.S.
Vogiannis and Nikolopoulos [13]	2008	-	-	○	○	Thermal spas in Greece	N.M.
Jelle [15]	2012	○	○	-	○	Sample calculations	N.S.S.
Arvela et al. [10]	1988	○	○	-	○	Finnish dwellings in summer and winter	N.S.S.
Font [5]	1997	○	○	○	○	Mediterranean climate house and Swedish house^b	N.M.
Font and Baixeras [6]	2003	○	○	○	○	Mediterranean climate house and Swedish house^b	N.M.

Table 1 Notation

Table 2 Summary of references reviewed in this article

^bThese applications were discussed in [7, 8]

Articles

Abstract

Keywords

Background

Review

Soil

1

2

3

Building material

4

Water for living

5

6

Ventilation between indoor and outdoor air

7

Ventilation among the compartments

8

Conclusions

Acknowledgements

NOTES

References

Figure & Data

REFERENCES

Citations

Fig. 1

Table 1

Table 2